[ Introduction | Description | Example 1 | Example 2 | Problems | References | Source Code | Further Info ]
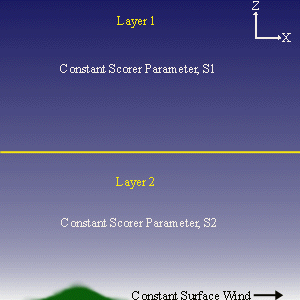
This work was a project for a seminar course (Fall 1995) on Visualization in Meteorology at Penn State University, taught by Dr. Peter Bannon. My chosen project's goal was to use Matlab to model (and then visualize) the two-dimensional airflow over an isolated mountain in the presence of an atmosphere with varying structure. More specifically, the atmosphere is idealized as a two-layer structure, where each of the two atmospheric layers has uniform profile as shown below.

Description:
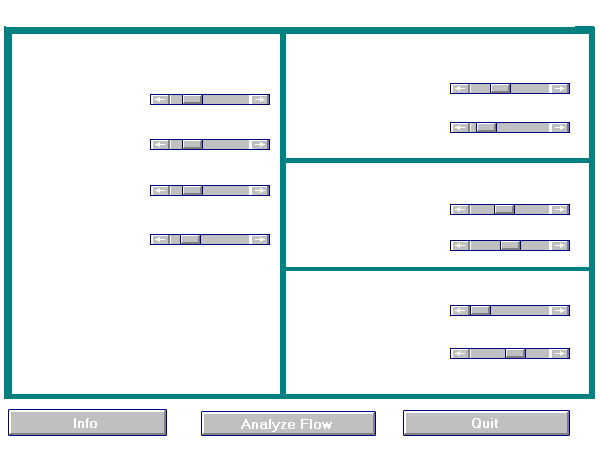
When the program is run, you are immediately given a menu. The menu is divided into 5 sections, and an example of the menu is shown in the figure below. The first section (left half) of the menu allows you to specify the atmospheric profile to be examined. Slider bars control the values for the surface wind speed, the Scorer parameter of each of the two layers, and the height of the two-layer interface. Based on the chosen atmospheric parameters, two non-dimensional numbers are displayed: the Scorer Condition and Rossby Number.
Scorer Condition - If this value is greater than 1, trapped waves will result.
The second section, in the upper left, describes the profile of the terrain over which the air flows. By altering the values in this section, you can specify terrain that resembles a small hill or a tall, steep mountain.
The third section, middle right, describes the profile of the domain. This allows you to zoom in or out on the mountain-perturbed airflow.
In the fourth section (lower right), you can specify the spectral profile of waves excited by the terrain. A typical run would use the default values (0 to 30 wavenumbers), which allows for excitation of all short and most long waves. However, you can focus on a specific range of waves--such as only short wavelengths or long wavelengths, to view the mountain flow if only that range of wavelengths are excited.
The final section includes the three buttons at the bottom. "INFO" gives a brief description of the model and the adjustable parameters. "ANALYZE FLOW" is pressed when the slider bars are set and you wish to examine the resulting airflow. Note that the two figures that appear may overlap one another on the screen. "QUIT" exits the program and closes the menu.
Examples:
Two sample runs of the model are given next. The output presented are exactly those provided by the model. The first example simultes airflow over a mountain in a uniform atmosphere which produces only vertical propagating waves, while the second example simulates airflow over a mountain in a non-uniform atmosphere which results in trapped waves.
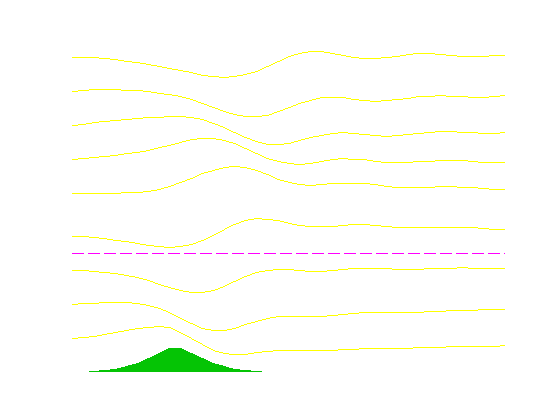
Example 1: Uniform atmosphere.
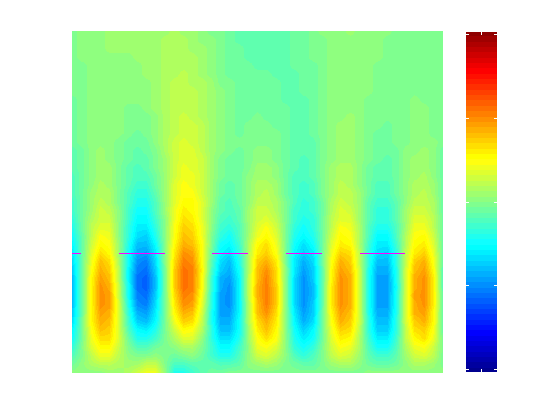
The first of two examples shows airflow over a mountain placed in a uniform atmosphere. The two layers of the atmosphere in the model have similar Scorer parameters. As a result, there is no reflection or refraction of waves at the layer interface. Therefore, all waves--both long and short--propagate vertically without reflection. However, since the wave propagation speed is dependent on wavelength (these are dispersive waves), the resulting mountain-perturbed airflow varies with height and distance.
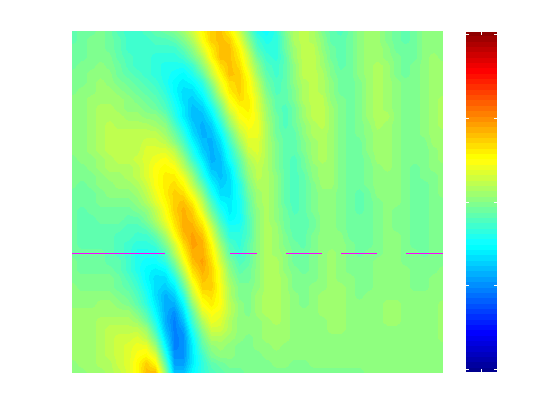
Example 2: Non-uniform atmosphere
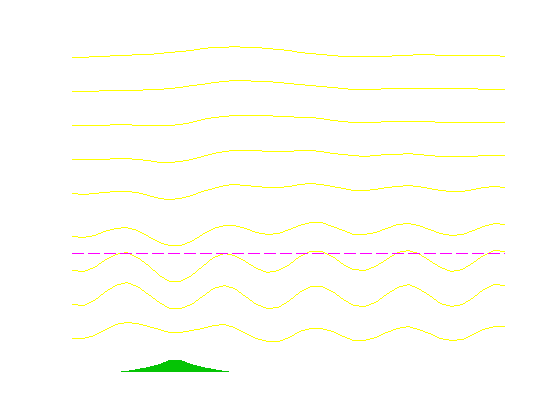
The second example demonstrates the model's simulation of trapped mountain lee waves. These waves are trapped because there exists a discontinuity at the layer interface (the Scorer Parameter changes between the layers, decreases from below to above the interface). Vertically propagating waves reflect when they encounter the interface, and downward propagating gravity waves result. Reflection occurs once again when the waves intercept the ground, and the process repeats, producing a train of lee waves. Since the upward and downward propagating waves in the lower layer have the same wavelength, the trapped waves have no horizontal tilt. Only certain wavelengths reflect at the layer interface, and this criterion is determined by the values of the Scorer parameters in the layers. For trapped waves to occur, a critical Scorer Parameter difference between the layers must exist. If this difference exists, the Scorer Condition (as shown in the menu) will be at least 1.
These trapped waves can often be seen in the atmosphere with your own eyes, or at least in satellite images. Often at the crest of the waves, saturation is reached and a cloud forms. If the waves are sufficiently trapped, the result is a series of nearly-parallel cloud rolls downwind of the mountain range, often up to several hundred miles away.
Here is the state of the menu when the flow was analyzed. Note the varying Scorer parameter--with the larger value in the lower layer.
Problems:
Two known problems exist:
1. The model analyzes the vertical velocity field by taking a finite set of waves (of varying wavelengths) and determines the amplitude of these waves when excited by the mountain in the specified atmospheric profile. Since the waves extend infinitely in the horizontal, the model can not distinguish between upstream and downstream, and non-physical upstream trapped waves often result. (These can be seen in Example 2, where trapped lee waves occur upstream of the mountain).
2. Certain combinations of mountain and atmospheric profiles can produce wave resonance, and numerical integration through Fourier analysis is unstable and the model produces exceptionally high values of vertical velocities. It is possible that such combinations are simple simulations of downslope windstorms in the Front Range of the Rocky Mountains. (This is also considered a feature!)
References on Mountain Waves:
For further and more detailed information on mountain waves and trapped lee waves, check out:
Alaka, M. A., 1960: The Airflow Over Mountains. WMO Technical Note No. 34. World Meteorological Organization, Geneva. 137pp.
Durran, D.R., 1986: Mountain Waves (Mesoscale Meteorlogy and Forecasting). American Meteorological Society, Boston, pp 472-492.
Gill, A.E., 1982: Atmosphere-Ocean Dynamics. Academic Press, New York, 662pp.
Gossard, E.E., and William H. Hooke, 1975: Waves in the Atmosphere. Elsevier, New York, 456pp.
Holton, J.R., 1992: An Introduction to Dynamic Meteorology. Academic Press, New York, 511pp.
Scorer, R. S., 1949: Theory of waves in the lee of mountains. Q. Jour. Royal Met. Soc., 75, 41-56.
Three subroutines comprise the model:
The model is run by executing the tlwmenu.m script.
For Further Information on the Model:
Bob Hart
Last Updated: March 1, 2018 to update scripts for newer Matlab versions.
Rossby Number - If this value is near or less than 1, Coriolis effects are significant and the model output should be used with caution since the model does not account for this deflection.

Matlab source code for model:
Florida State University Meteorology
rhart@fsu.edu